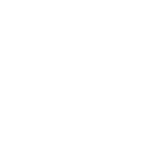设想一下,如果你是一名城市规划师,负责为一座大城市在最佳位置建设两个机场,在保证全市每个居民区到最近机场的距离尽可能短的前提下,机场应当如何选址?这一案例源自计算几何领域中的一个经典优化问题——平面内双中心问题(Planar Two-Center Problem)。
近日,上海纽约大学计算机科学助理教授薛杰与合作者共同研发出一套解决平面内双中心问题的新算法。该算法能够以最快速度计算出问题的最优解,解决了计算几何领域的这一经典的基础性难题。今年6月,在希腊雅典举办的第40届国际计算几何算研讨会(SoCG 2024)上,该项研究成果被收录于大会的论文集中。
计算几何是理论计算机科学的一个分支,专注于用算法解决点、线、面和其他几何形状相关的问题。平面内双中心问题的目标是在平面上找到两个最小的等大小的圆使其可以覆盖平面上给定的所有点。在机场选址的应用中,城市可被视为平面,各个居民区则是平面上的点,两个机场的位置为两个圆的圆心。选址目标是确定机场(即圆心)的位置,从而最小化居民到较近机场的最大距离。
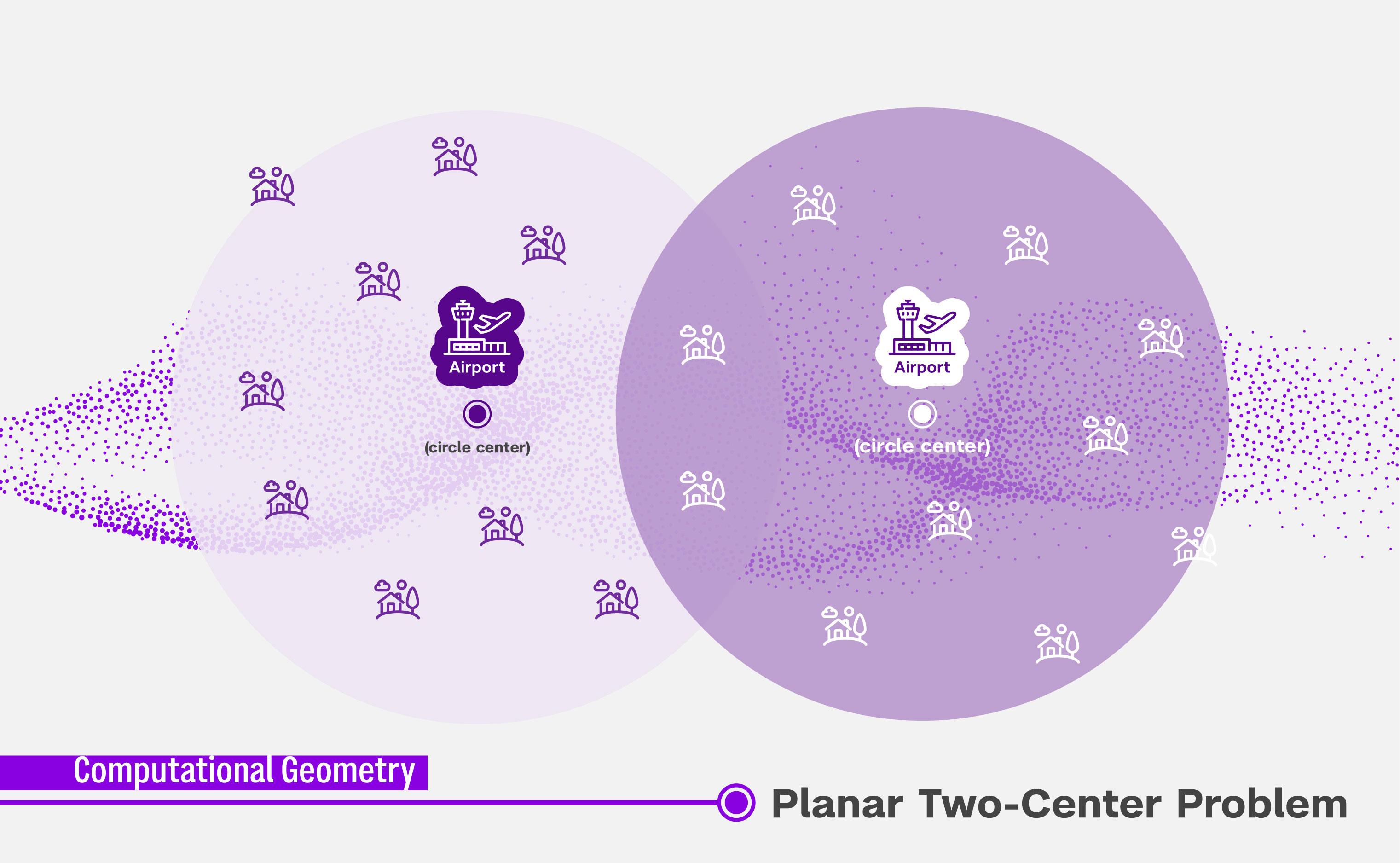
平面内双中心问题的求解过程需要大量繁复耗时的计算。几十年来,科学家们一直在开发更高效的算法,以期在更短时间内计算出最优解。薛教授介绍说:“自上世纪80年代以来,平面内双中心问题便悬而未决。到1997年,科学家得出了计算最优解所需时间的一个下界。此后近30年中,研究者以达到该时间下限为目标,不断对已有算法进行优化,然而取得的进展十分有限。”
在本项研究中,薛教授同韩国浦项科技大学的Kyungjin Cho和Eunjin Oh教授,以及美国犹他大学的王海涛教授合作,开发出了一种解决平面内双中心问题的新算法,极大地改进了现有结果。这是自1997年以来几十年的努力研究后,首个被提出的时间复杂度与下限值相匹配的算法,标志着计算几何领域的重大突破。薛教授说:“虽然这一研究理论性很强,但该算法实际上能够在解决城市规划等现实问题中进行应用,并有望推动对两个以上的多中心问题的探索。”
在SoCG 2024大会上,除该项研究外,薛教授还有四篇论文被收录进集,成为今年唯一一位入选论文数达到五篇及以上的参会学者。这些论文各有侧重,其核心都是为几何问题开发高效算法。其中,题为“An O(nlogn)-Time Approximation Scheme for Geometric Many-to-Many Matching”(编者注:几何多对多匹配的O(nlogn)时间近似方案)的论文获得了该会议的最佳论文奖(Best Paper Award),这也是中国大陆学者首次在SoCG大会上获此殊荣。会上,薛教授远程展示了两篇被收录的论文,并与感兴趣的听众展开热烈讨论。